Injektive funksjoner
En funksjon er injektiv dersom hver verdi du putter inn som x gir forskjellig verdi for y.
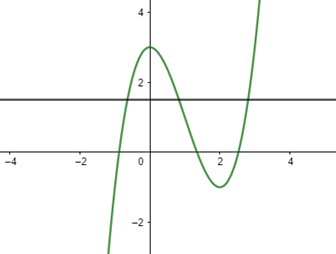
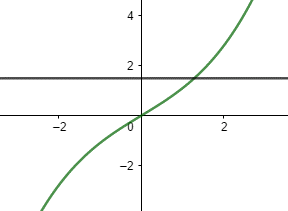
En måte sjekke om en funksjon \(f(x)\) er injektiv, er å tenke deg at du flytter en horisontal linje oppover og nedover og sjekker hvor mange steder den krysser grafen til \(f(x)\). Dersom linja på noe tidspunkt krysser grafen til \(f(x)\) i to punkter eller mer, er \(f(x)\) ikke injektiv: