Inverse funksjoner

For å vise at noe er en invertert funksjon pleier man å opphøye i -1 i funksjonsnavnet:

Dette har ikke noe med den matematiske operasjonen å opphøye noe i -1 å gjøre, det er bare en måte å vise at det er en invers funksjon.

Når du inverterer en funksjon, finner du en annen funksjon som går «andre vei». La oss si at du i en funksjon \(f(x)\) setter inn et tall \(A\) som x-verdi, og du får ut et tall \(B\). Hvis du deretter setter inn tallet B i \(f^{-1}(x)\) (inversen til \(f(x)\)), vil du få ut tallet \(A\)!

Dette kan skrives slik: \(f(A)=B \Leftrightarrow f^{-1}(B)=A\)

Dette betyr også at: \(f(f^{-1}(x))=x\)

For å invertere en funksjon \(f(x)\) kan du bruke denne metoden:

La oss gjøre dette for \(f(x)=2x+3\):

1. Vi skriver om til: \(y=2x+3\)
2. Vi løser denne likningen for x og får: \(x=\frac{y-3}{2}\)
3. Vi bytter ut navnene og får: \(f^{-1}(x)=\frac{x-3}{2}\)

Når man inverterer en funksjon, vil grafen til funksjonen bli speilet om linjen \(x=y\).

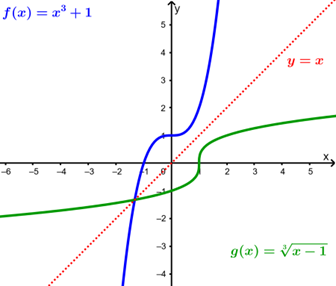
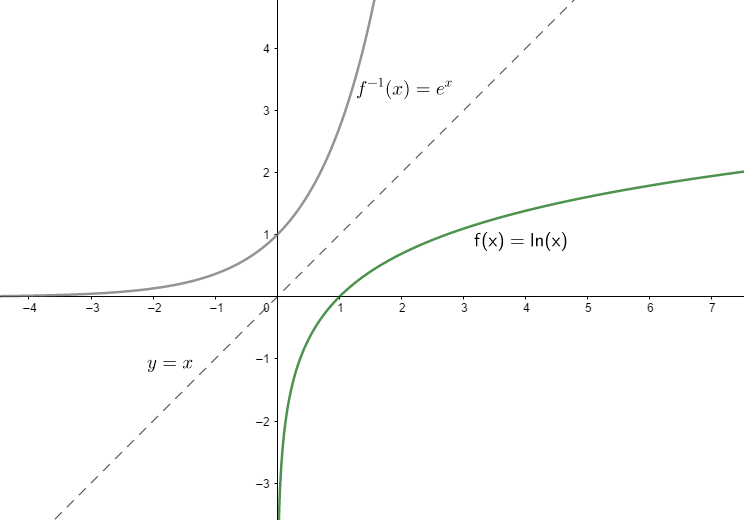
Hvis du tenker veldig hardt over hva den inverse funksjonen gjør, kan du (kanskje) forstå hvorfor den ser slik ut.

Funksjoner som ikke er injektive kan ikke inverteres. Dette er fordi funksjoner som ikke er injektive har flere x-verdier som gir samme y-verdi. Da vil den inverterte funksjonen ha flere y-verdier for en x-verdi, og dette er ikke lov for "vanlige funksjoner" (Funksjoner på formen \(f: \mathbb{R} \rightarrow \mathbb{R}\))

For å invertere funksjoner som ikke er injektive må man derfor begrense definisjonsmengden, slik at funksjonen er injektiv på hele området den er definert.