Newtons Metode
Newtons metode er en metode for numerisk likningsløsning. Dette vil si at den kan brukes til å løse likninger som er vanskelige eller umulige å løse analytisk. Metoden er iterativ, som vil si at man gjør en matematisk operasjon mange ganger på rad, og kommer (forhåpentlig vis) nærmere og nærmere løsningen på likningen for hver iterasjon.
Metoden gir en tilnærmet verdi for nullpunktene til en funksjon, som vil si at den gir en tilnærmet løsning til likningen \(0 = f(x)\), der \(f(x)\) er en hvilken som helst deriverbar funksjon.
Hvordan fungerer Newtons metode?
For å løse likningen \(0=f(x)\) med newtons metode starter man med å velge en x-verdi \(x_n\). Deretter finner man tangenten til funksjonen \(f(x)\) for denne x-verdien. Den x-verdien der tangenten krysser x-aksen kaller vi \(x_{n+1}\).
\(x_{n+1}\) vil i de fleste tilfeller være nærmere nullpunktet til \(f(x)\) enn \(x_n\) (se figur 1).
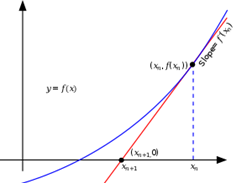
Vi kan gjøre denne prosessen mange ganger, ved å sette inn verdien vi fikk for \(x_{n+1}\) som \(x_n\) i neste iterasjon. Når man gjør dette mange ganger vil man som oftest få en verdi som kommer veldig nær nullpunktet til \(f(x)\). Figur 2 viser hvordan dette ser ut grafisk.
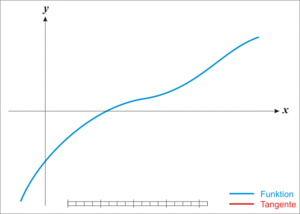
For å finne et utrykk for \(x_{n+1}\) kan man bruke utrykket for tangenten til en funksjon, og sette dette lik null for å finne hvor tangenten krysser x-aksen.
Ved å bruke ettpunktsformelen, finner vi at utrykket for tangenten til \(f(x)\) ved x-verdien \(x_n\) er:
\[y=f(x_n)+(x-x_n)f'(x_n)\]
Nå må vi finne ut hvor denne linja krysser x-aksen, og dette gjør vi ved å sette \(y = 0\), og deretter løse for \(x\). Da ender vi opp med:
\[x = x_n - \frac{f(x_n)}{f’(x_n)}\]
Hvordan bruke newtons metode?
Hvis man vil løse en likning ved å bruke Newtons metode, må man først skrive om likningen til formen \(0=f(x)\). Dette kan man gjøre enkelt ved å flytte alle leddene i likningen til høyre side.
Deretter må man finne \(f’(x)\). Dette gjør man ved å derivere den høyre siden av likningen \(f(x)\). I noen tilfeller kan det være vanskelig å derivere \(f(x)\), da kan man bruke numerisk derivasjon (Link til side).
Etter dette gjør man iterasjonen \(x_{n+1} = x_n - \frac{f(x_n)}{f’(x_n)}\). Du velger selv hvilken verdi \(x_n\) skal ha i første iterasjon. I hver ny iterasjon settes forrige verdi vi fikk for \(x_{n+1}\) inn som \(x_n\).
Det er bra å velge en initialverdi for \(x_n\) som er så nærme løsningen på likningen som mulig. Det vil si, hvis du tror at svaret på likningen er omtrent \(x=3\), ikke sett initialverdien til \(x_n = 30000\).
Eksempel på bruk av Newtons metode.
Eksempel: Løs likningen \(x = \cos(x)\) ved hjelp av newtons metode.
Steg 1: Først skriver vi om likningen slik at det står 0 på venstre side. Da ender vi opp med: \(0 = cos(x)-x\)
Steg 2: Deretter finner vi \(f’(x)\) ved å derivere \(f(x)\) (den høyre siden av likningen). \(f(x)\) er i dette tilfellet \(\cos(x)-x\), så da får vi at \(f’(x) = -1-\sin(x)\)
Steg 3: Nå er det på tide å iterere! Vi velger en initialverdi på 1 for \(x_n\). Deretter starter vi med første iterasjon:
\(x_{n+1}= x_n - \frac{f(x_n)}{f’(x_n)} = 1 – \frac{\cos(1)-1}{-1-\sin(1)} \approx 0.7504\)
Etter dette fortsetter vi med andre iterasjon. Denne iterasjonen er helt lik, bortsett fra at vi setter inn verdien for \(x_{n+1}\) vi nettop fikk som \(x_n\):
\(x_{n+1}= x_n - \frac{f(x_n)}{f’(x_n)} = 0.7504 – \frac{\cos(0.7504)-0.7504}{-1-\sin(0.7504)} \approx 0.7391\)
Denne prosessen gjentas helt til du har en verdi som er «presis nok».
Siden det er ekstremt tungvint å skulle gjøre alle disse iterasjonene for hånd, pleier man å skrive et python-script som gjør jobben for deg. Jeg gjorde 1000 iterasjoner med newtons metode på denne likningen i Python, og fikk at \(x=0. 739085133)\)
Når fungerer Newtons metode?
Newtons metode fungerer ikke dersom \(f’(x_n) = 0\) i noen av iterasjonene. Da får man divisjon på 0, noe som fører til error.
Det er også noen funksjoner der Newtons metode ikke funker særlig bra. Nedenfor er det vist et eksempel på en slik funksjon:
