Numeriske metoder for differensiallikninger
Det finnes mange metoder for å løse differensiallikninger numerisk, her skal vi gå igjennom noen av dem.
Euler's eksplisitte metode
Euler’s eksplisitte metode (ofte bare kalt Euler’s metode) er en numerisk metode som vi kan bruke til å løse differensiallikninger.
For å bruke Euler’s metode trenger man to ting:
- En differensiallikning som kan skrives på formen \(\dot{y} = g(y)\), der \(g(y)\) er en hvilken som helst funksjon av \(y\)
- En initialverdi for \(y(t)\), for eksempel \(y(0)=3\)
Med disse opplysningene kan vi bruke Euler’s metode til å lage en graf for funksjonen \(y(t)\). Vi kommer ikke til å ende opp med et utrykk for \(y(t)\), slik som man hadde gjort dersom man hadde løst differensiallikningen analytisk. Det vi ender opp med er en liste med y-verdier, og disse y-verdiene kan vi plotte for å se hvordan grafen \(y(t)\) ser ut.
Hva vet vi om grafen til \(y(t)\) ut ifra opplysningene vi har? Vi vet både hva \(y(0)\) er, og hvis vi setter inn \(y(0)\) i utrykket vi har for \(\dot{y}\), vet vi også hva stigningstallet til grafen er når \(t=0\). Dette kan vi bruke til å finne en approksimasjon av hva \(y(0.1)\) må være.
Stigningstallet til en graf sier (veldig uformelt) hvor mange skritt du må gå oppover for hvert skritt du går bortover. Hvis vi nå vil vite hva \(y(0.1)\) er, kan vi bruke dette. I \(y(0.1)\) har vi bevegd oss \(0.1\) skritt bortover. Det vil si at vi må gå \(0.1 \cdot \dot{y}\) skritt oppover. Da får vi:
\[y(0.1)=y(0)+0.1 \cdot \dot{y}\]
Ut ifra differensiallikningen vet vi at \(\dot{y}=g(y)\), som vil si at vi kan skrive om denne likningen til:
\[y(0.1)=y(0)+0.1 \cdot g(y(0))\]
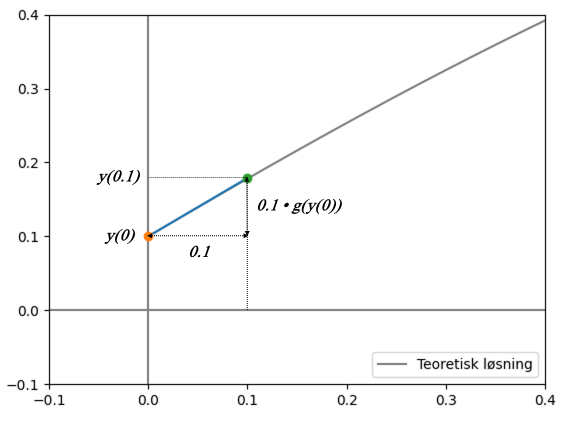
Vi kan bruke samme formel igjen for å finne \(y(0.2)\), ved at vi setter inn verdiene vi fant for y(0.1), og får:
\[y(0.2) = y(0.1) + 0.1 \cdot g(y(0.1))\]
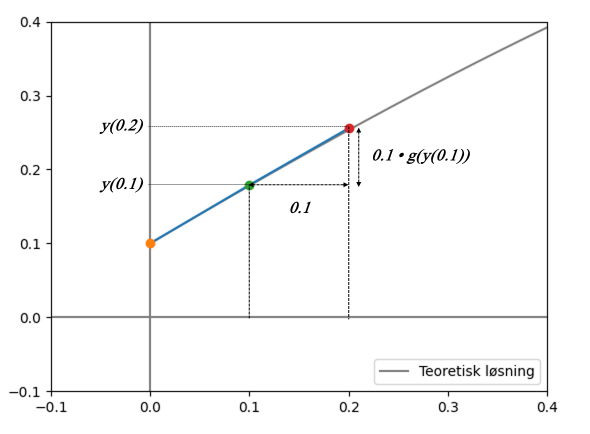
Hvis vi fortsetter på denne måten, og legger til alle y-verdiene i en liste, vil vi ende opp med nok y-verdier til å plotte grafen til \(y(t)\).
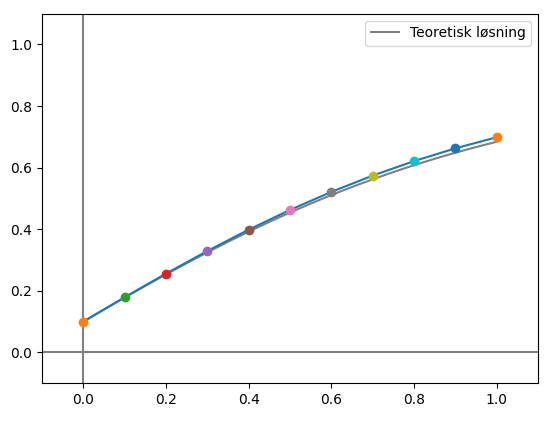
Siden vi bruker verdiene fra forrige iterasjon hver gang vi regner ut en ny iterasjon er dette en iterativ metode, og vi kan skrive formelen vi har brukt som et iterativt utrykk:
\[y_{n+1} = y_{n}+h \cdot g(y_{n})\]
I utrykket over representerer variabelen h hvor langt vi beveger oss langs t-aksen for hver iterasjon. Vi kan selv velge verdien til h. Dersom man velger en mindre verdi for h, vil grafen bli mer presis, men man må også gjøre flere iterasjoner for å plotte like stor tidsmengde. Det kan vises at avviket man får med Euler's metode i gjennomsnitt er proporsjonalt med h. Det vil si at hvis man velger dobbelt så stor h, vil feilen man får i approksimasjonen i gjennomsnitt være dobbelt så stor.
Under er det et kodeeksempel på hvordan Euler's metode kan implementeres i Python.
import numpy as np
import matplotlib.pyplot as plt
# g(y) er det som står på høyre side av likningen når y' står alene på venstre side.
def g(y):
return 1-y**2
maxT = 10 #Plottet av grafen starter i t=0, og slutter i maxT
steps = 10000 #Hvor mange skritt vi skal ta, høyere verdi = bedre resultat men saktere
h = maxT/steps #Lengden av hvert skritt
y = [3] #Lager en liste med y-verdier til grafen til y(t), første element er initialverdien y(0)
ts = [0] #Lager en liste med t-verdier
for n in range(steps):
ts.append((n+1)*h) #Listen med t-verdier starter på 0, og for hver iterasjon legger vi på (n+1)*h, slik at den ender opp som [0, 1h, 2h, 3h, 4h ... ]
y.append(y[n] + h*g(y[n])) #Her bruker vi formelen for y_(n+1) til å legge til neste y i lista som heter y.
plt.plot(ts, y)
plt.show()
Euler's implisitte metode
Eulers implisitte metode er ikke nødvendigvis bedre enn eulers eksplisitte metode, men det er viktig å forstå den for å kunne bruke metoder som faktisk er bedre, for eksempel trapesmetoden.
Eulers implisitte metode likner veldig på eulers eksplitte metode. Den eneste forskjellen er at det nå står \(y_{n+1}\) inni \(g(x)\), istedenfor \(y_n\):
\[y_{n+1} = y_{n} + h \cdot g(y_{n+1})\]
Det er ett problem med likningen over, nemlig at \(y_{n+1}\) står på både høyre og venstre side av likningen. Da kan vi ikke bare sette inn \(y_n\) og finne hva \(y_{n+1}\) er, slik som man gjør i Euler’s eksplisitte metode. Istedenfor må vi se på iterasjonsutrykket som en likning, der \(y_{n+1}\) er den ukjente, og vi må ha løsningen på denne likningen hver gang vi skal legge til en ny y-verdi i listen over y-verdier.
Det er to måter man kan gå frem for å løse denne likningen, analytisk og numerisk. Vi skal nå gå igjennom begge disse måtene.
Analytisk
I mange tilfeller kan man løse likningen \(y_{n+1} = y_n+h*g(y_{n+1})\) analytisk for \(y_{n+1}\). For eksempel, dersom \(g(y)=2y+1\), vil man få følgende likning:
\[y_{n+1} = y_n + h(2y_{n+1}+1)\]
Dersom vi løser denne likningen for \(y_{n+1}\) får vi følgende:
\[y_{n+1}=\frac{y_n+h}{1-2h}\]
Nå har vi et utrykk der vi kan sette inn verdiene for \(h\) og \(y_n\) og finne ut hva \(y_{n+1}\) er. Dette utrykket kan vi bruke til å finne punkter på grafen til \(y(t)\). Det er viktig å huske at utrykket vi fant nå kun fungerer dersom \(g(y)=2y+1\). Dersom \(g(y)\) er noe annet (som den mest sansynlig er), må vi sette opp likningen på nytt og løse for \(y_{n+1}\).
Numerisk
Noen ganger er \(g(y)\) slik at det er umulig å løse \(y_{n+1} = y_n+h*g(y_{n+1})\) analytisk. Da må vi løse den med en numerisk metode, for eksempel newtons metode. For at notasjonen her ikke skal bli alt for forvirrende skriver vi om likningen \(y_{n+1} = y_n+h*g(y_{n+1})\) til \(x = y_n+h*g(x)\). For å løse denne likningen med newtons metode kan vi gå frem som følgende (se temaside om Newton’s metode):
1: Skriv om likningen til formen \(0 = f(x)\):
\[0 = -x +y_n+h*g(x) = f(x)\]
2: Finn \(f’(x)\):
\[f’(x) = -1 + h*g’(x)\]
3: Velg \(y_n\) som initialverdi for x_n, og gjør iterasjonen \(x_{n+1} = x_n-\frac{f(x_n)}{f’(x_n)} \) helt til du har funnet er presist nok svar på likningen (når jeg testet holdt det ofte med 5 iterasjoner).
Dette vil gi oss en verdi for \(x\), som vil si at vi har funnet en verdi for \(y_{n+1}\).
Når vi har funnet \(y_{n+1}\) med enten numerisk eller analytisk løsning av likningen, kan vi legge til \(y_{n+1}\) i listen over y-verdier til \(y(t)\).
Trapesmetoden
Når man løser en differensiallikning med Newton’s eksplisitte og Newton’s implisitte metode, vil grafen man får med hver av metodene nesten alltid havne på forskjellige sider av den teoretiske løsningen på differensiallikningen.
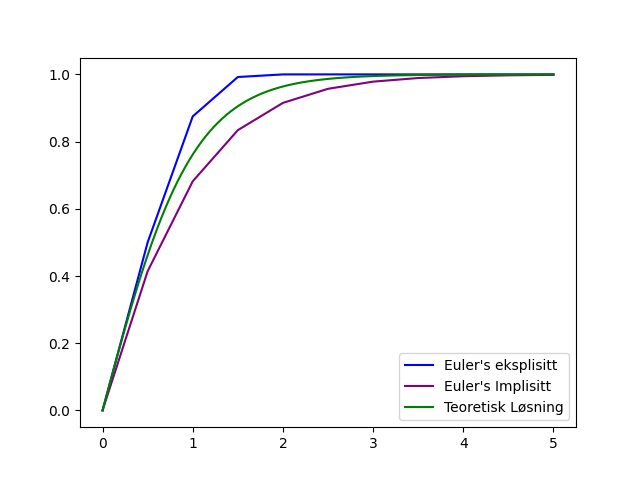
Grunnen til dette er at Euler’s eksplisitte bestemmer \(y_{n+1}\) basert på hva \(\dot{y}\) er ved starten av skrittet, i motsetning Euler’s implisitte som bestemmer \(y_{n+1}\) basert på hva \(\dot{y}\) er ved slutten av skrittet. En fremgangsmåte for å få en bedre approksimasjon, er å bruke gjennomsnittet mellom \(\dot{y}\) i starten og slutten av skrittet. Denne metoden kalles trapesmetoden:
\[y_{n+1}= y_n+h(\frac{g(y_n)+g(y_{n+1})}{2}) \]
Siden denne metoden har \(y_{n+1}\) på begge sider av likhetstegnet, må man løse den som en likning på samme måte som Euler’s eksplisitte metode.
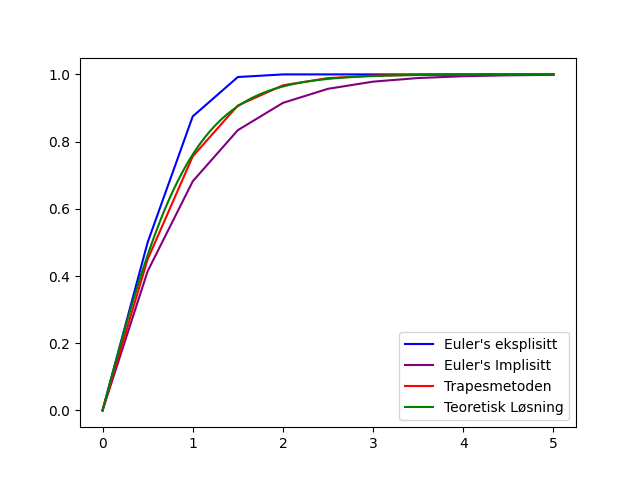
Som vi kan se på figuren, gir trapesmetoden som regel en bedre approksimasjon enn Euler’s eksplisitte og implisitte metode.
Heuns metode
Heuns metode ligner veldig på trapesmetoden, men man bruker et «triks» for å slippe å ha \(y_{n+1}\) på begge sider av likningen. Dette «trikset» er basert på Euler’s eksplistte metode.
Trapesmetoden sier:
\[ y_{n+1}= y_n+h(\frac{g(y_n)+g(y_{n+1})}{2}) \]
Euler’s eksplisitte metode sier:
\[y_{n+1} = y_{n}+h \cdot g(y_{n}) \]
For å bli kvitt \(y_{n+1}\) på høyre side av trapesmetoden, kan vi bruke det Euler’s eksplisitte metode sier, og bytte ut \(y_{n+1}\) med \(y_{n}+h \cdot g(y_{n})\). Dette gir oss Heuns metode.
Heuns metode:
\[y_{n+1}= y_n+h(\frac{g(y_n)+g(y_{n}+h \cdot g(y_{n}))}{2}) \]
Fordelen med å bytte ut \(y_{n+1}\) er at man ikke lenger trenger å løse iterasjonslikningen numerisk eller analytisk slik som man må i trapesmetoden. Derfor vil Heuns metode være raskere enn trapesmetoden dersom \(g(y)\) er avansert nok til at man må bruke numerisk likningsløsning i trapesmetoden.
